The study of set theory is one that is deep and often covered in music theory courses devoted to the analysis of 20th century music. A “nutshell” description of it is here. The typical approach to pitch set analysis involves considering pitches numerically (0=C, 1=C#, etc.), understanding the different pitch-class sets that are possible (there are 208!) considering three-note collections (trichords), four-note (tetrachords), five-note (pentachords), and so forth, with each set representing both the notes in “proper” order and under both ansposition and inversion, as is the common practice.
Why use set theory as a composer?
One point of set theory is to create a “language” for understanding music that is not based on triads as a fundamental feature of melody and harmony. Indeed, pitch sets are used like notes of a chord — they can be a framework for melodies, stacked as chords, embellished, and so forth. The order of pitches isn’t what is important (as it is with twelve-tone music).
For instance, music could be composed that features the pitch-class set 0,1,4 (it’s called “3-3,” since it is listed third on the standard table of pitch-class sets), transpositions of that set, and inversions of it:

3-3 is, in fact, a main feature of the second movement of Bartok’s String Quartet No. 2. We can most easily see this by looking at the intervals between notes of the piece; when motives are framed by a major third that is divided by a half-step on one side or the other, it is “3-3,” like in this music at rehearsal 1:

This passage also has a couple of extra notes – the G# in bar 19 helps expand 3-3 into more of a scale, as does the C# in bar 23. The C# in bar 23 also helps make another version of 3-3 (0,1,4 transposed up by a half step).
Another way that Bartók used this trichord is as main notes of the melody in rehearsal 4:

At rehearsal 7, this trichord is found alongside 3-4 (0,1,5 – imagine a perfect fourth with a half step-in the middle, like C-C#-F or C-E-F).

At bar 116, there is a very strong chord that combines 3-3 and 3-4 into a single unit.
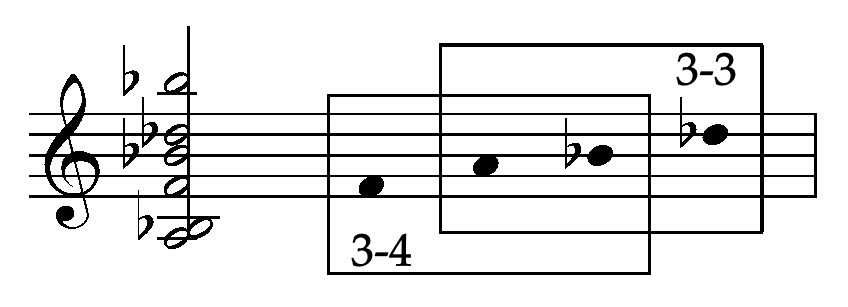
As the music continues from this point, the cello performs a melody that also blends 3-3 and 3-4.

…and forth it continues.